首页>技术中心>技术资讯>脉冲调宽乘法器在交流应用下的误差及标准功率、电压、电流测量仪的研制
脉冲调宽乘法器在交流应用下的误差及标准功率、电压、电流测量仪的研制
发布时间:2017-09-01
脉冲调宽乘法器用于测量直流电压时可以达到很高的准确度,但在交流测量领域中却较少用于电压、电流的测量,只在工频功率/电能测量方面有较多应用。作者现就近年来研制标准功率、电压、电流测量仪过程中涉及的脉冲调宽乘法器(PWMM)的误差问题作某些探讨,并介绍该测量仪的设计方案及实验结果。
1脉冲调宽器(PWM)在交流应用下的误差
对交流信号进行脉冲调宽变换的方案很多,可归纳为4大类:1)三角波电压比较型,如RM11型标准电能表;2)节拍方波控制的电压积分型,如2855型功率/电压变换器;3)无节拍方波控制的电压积分型,如TVL21型功率/电压变换器;4)无节拍方波控制的电流积分型。
关于以上各类PWM的原理及优缺点比较,可参考文献[1]。作者研制的高精度功率、电压、电流测量仪选用无节拍方波控制的电流积分型PWMM方案,这种方案易于克服电子开关内阻及运放失调所带来的误差,电路结构简单,性能/价格比好,采用国内市场上的通用元器件就较好地达到了预期的指标。
1・1PWMM交直流变换误差与在一个信号周期Ts内分割次数N的关系
当PWMM工作在直流信号Iu下,其工作原理如图1、2所示。在图1中,Iu为直流电流信号,IR为由恒流源提供的基准电流,|IR|>|Iu|。若积分器是理想的,则其输出电压uC(t)作线性变化。对电流和Iu+IR积分时,当uC(t)下降至阈值比较器下限UTL时比较器翻转,输出的控制信号反向,使IR切换成-IR,积分器转为对电流差Iu-IR积分,直至uC(t)上升至阈值比较器上限UTH时比较器再度翻转,如此周而复始。
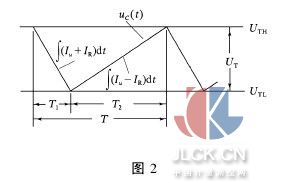
式中: T=T1+T2,即一次调宽时间;如T是不变的,则可称之为脉冲调宽器的分割周期。
为脉冲调宽信号,它是一串其脉冲宽度受Iu控制的脉冲信号。若用±ξ(Iu)去控制图3所示的模拟开关桥,则当在桥的一个对角中输入被乘信号电流Ii时,在桥的另一对角的负载电阻R上将得到如图4所示的电流波形,它由幅度为Ti、持续时间分别为T2、T1的正、反向电流脉冲所组成。由于T2≠T1,这正、反向电流的平均值为
式(5)表明,开关桥输出电流的平均值(可通过滤波器获得)-I正比于两个信号电流Iu与Ii的乘积。-I与乘法器中电容C及UTH-UTL=UT的值无关,因而不受元件参数的影响,只与基准电流IR有关。
它与积分电容C及UT、IR有关,亦与输入信号Iu有关。
当输入PWM交流电流iu(t)=Iumsinωt时,每个瞬时的iu(t)都是不同的,如图5所示,在tk→(tk+Tk1)这一时段内被积分的是iu(t)在此段内的一段弧,而在(tk+Tk1)→(tk+Tk)的时段内则为另一段弧,两者均不能以简单的直流平均值代替,而必须用积分公式来准确表达调宽过程:在uC(t)向下变化时有
在上式中,从某一时刻tk开始的一次分割时间为Tk=Tk1+Tk2,它与积分开始时刻tk有关,例如,在ωt=0°、180°附近,Tk最短;而在ωt=90°、270°附近,Tk最长。Tk随iu(t)作周期性的伸长、缩短。
在从时刻tk到tk+1(即tk+Tk)的时段内,若模拟开关桥的输入信号电流也为正弦波:ii(t)=Iimsinωt,则在ξ(iu)的控制下,开关桥的输出电流i在该时段内的平均值为
设在一个信号周期TS=2π/ω内有N次分割(N并非一定是整数),则开关桥在TS内输出电流的平均值为
将式(9)、(10)代入式(12),得
式(13)是PWMM工作在正弦信号下的准确计算式,它不同于直流信号情况下的式(5)。从形式上看,PWMM似乎不是实现了两信号的相乘,而是相除。问题实质在于式(13)中反映了一个信号周期TS内的时段分割数N对-I的影响,从物理意义上讲, N→∞时iu(t)与ii(t)才真正实现的是瞬时值对应地相乘,N越小则偏差越大。目前有许多文献将PWMM在交流下的输出表达为
但这只是近似式,不反映出N对-I的影响。可以证明,若以有效值Iurms代替直流值Iu代入式(6)求出分割周期Trms,并以后者代替TS/N=-Tk(-Tk为TS时段内各Tk的平均值),则也可将式(13)转化为式(14)。显然,这种替代反映了式(13)与式(14)定性上的一致,但式(14)并不准确。
式(13)虽然准确,但由于N与C、VT、IR均有关,因此直接应用式(13)去计算-I是困难的。作者设定不同的C、VT、IR、IirmsIurms及TS,藉助PC机应用迭代法及双精度运算,求出了在不同分割数N下式(13)与式(14)计算结果的相对误差γ,如表1所示。由表1可见,γ与N有关;若所设计的乘法器N>400,则此乘法器的输出电流-I完全可以用式(14)计算,乘法器的误差极小。但要实现N>400,往往受电子器件响应速度的限制。事实上,只需选用小的电容C及阈值UT,就可随意使N增大,但若器件响应速度不能与之相应,则效果将适得其反。
文献[2]给出了测量功率时与N有关的误差公式
若以表1中所用诸N值代入式(15),计算结果如表2所示。可见表2与表1的数据十分相近。
作者以自行设计的PWMM在N=200时的-I作为基准参考值,实际测定N小于200时相对于前者的误差,结果如表3所示。表3给出的实验数据验证了式(13)及式(15)的正确性;虽然限于实验条件,数据不能做到十分精确,并且受器件响应速度限制,N>200的实验未能精确进行,但也观察到N>200后相对于N=200时的值显然已是负值,且随N的增大其变化越来越缓慢,其规律与表2、3所示的规律是一致的。
由此可以得出以下3点结论:1)若N不够大,则PWMM产生正误差;N过小时,误差急剧上升。2)若可实现N≥200的电路设计,则PWMM的误差将小于2×10-5。3)在C、UT已选定的条件下,取IR≥(3~4)Iu的额定值,实验表明,PWMM对于不同大小的输入信号Iu将有较好的线性度。理论上,IR≥(3~4)Iu可避免出现IR-iu过小的情况,使积分器输出电压的工作线段十分靠近指数曲线的最初始段,即非常接近于直线。
1・2脉冲调宽器的相移Δφ
脉冲调宽乘法器的相移误差主要源于实际电路的延时效应,图1中的积分器、阈限比较器、电流开关等均存在动态延迟,设其正向综合延迟为Δτ,反向综合延迟为Δτ′。如图6所示,由于Δτ的存在,uC(t)下降至UTL时,IR要经过Δτ延迟后才切换成-IR;同样,在uC(t)上升至UTH后,也要经过Δτ′延迟才切换电流方向。这样,在UTH、UTL两个方向就分别产生了uC(t)超越UTH、UTL的过冲ΔUTH及ΔUTL。
前已述及UT的大小并不影响PWMM的准确度,因此UT扩大为U′T是无害的。但当ωt≠0时,例如ωt=90°时,iu=ium,uC(t)下降斜率最大(对应于Ium+IR)及上升斜率最小(对应于Ium-IR),因此对于ΔUTL还要在Δτ・IR/C上附加一项近似为Δτ・Iumsin90°/C的增量,而对于|ΔUTH|则减小Δτ・Iumsin90°/C。这说明,由于Δτ、Δτ′的存在,实际的阈值已不再是恒定值,受到输入信号iu(t)的调幅。这相当于式(7)等号右项中出现了增量Δτ・Iumsinωt/C,式(8)等号右项中出现了增量Δτ′・Iumsinωt/C,或相当于式(7)、(8)等号右边分别出现了附加积分。
式中: m、n为很小的常量。相对于iu(t)=Iumsinωt而言,-Iumcosωt是滞后于前者90°的信号,其作用使Iu产生滞后的Δφ。
实验表明,当Δτ、Δτ′较大时,在示波器上可以观察到具有包络线的uC(t)波形,而当采取措施使Δτ、Δτ′下降时,包络线逐渐减小,甚至难以观察到它。实验还表明,简单的PWM电路可使Δφ达到0・05°~0・1°,而良好的电路设计可使Δφ下降至0・01°~0・03°。实验证明,若在阈值比较器输入端叠加一个微小而适量的与-Iumsinωt成正比的电压附加信号,可以补偿Δφ的存在。文献[3]中用这种办法补偿PWMM型功率/电压变换器的相位误差。
1・3PWM的“真”恒流源工作方式问题
式(1)、(2)及式(7)、(8)均建立在用真恒流源信号对电容C充、放电的前提下,否则即使输入信号为直流Iu,uC(T)也将是指数曲线,ξ(Iu)不再是线性函数,PWMM的输出电流I将不再符合式(5),从而产生误差。
现在常见的应用于功率测量的PWM电路,其基准电流IR具有较好的恒流源特性,等效内阻可达10~20MΩ。但其iu(t)输入电路的等效内阻一般为100kΩ,结果不仅使PWMM的误差相当大,同时还造成功率变换器的电压线性度下降。因此,若要使PWMM的误差小且电压线性度好,以便用于电压测量,采用等效内阻很高的信号输入电路是十分必要的。
2功率、电压、电流测量仪的原理框图及误差综合
以上述对PWMM误差因素的分析为依据,作者设计研制了功率、电压、电流测量仪。
2・1测量功率的原理框图
图7是测量功率P的原理框图。在图7中,输入电压Uin经具有高输出阻抗的u/i变换器变换成iu(t)后,再经电流互感器CT1输入PWM。输入电流Iin经CT2变换为ii(t),通过模拟开关桥实现与iu(t)相乘,输出平均值为-I=IuIicosφ/Ik的电流,再经I/f变换器变换为与-I成正比的频率f,单片机μc接收f信号,经运算后显示被测功率值。这里Iu为iu(t)的有效值,Ii为ii(t)的有效值。
2・2测量交流电压的原理框图
图8是测量交流电压Uin的原理框图。在图8中,输入电流的CT2与PWMM脱离,而将辅助电流互感器CT3与CT1串联运行。此时PWMM的输出为-I=I2u/R,经μc开方处理后使显示器显示被测电压Uin的有效值。
2・3测量交流电流Iin的原理框图
图9是测量交流电流Iin的原理框图。在图9中,将电压输入电路与PWMM脱离,而使CT2与CT1串联运行。此时PWMM的输出为-I=I2i/IR,经μc开方后使显示器显示被测电流Iin的有效值。
以上各原理框图中, u/i变换器,电流互感器CT1、CT2、CT3,基准电流IR,I/f变换器等的误差均可控制在1×10-5~3×10-5的范围内,μc的运算误差亦可小于1×10-5,由于应用了对PWMM误差分析得出的指导性原则,研制成功的PWMM误差在2×10-5~4×10-5范围内。误差的综合计算表明,作者所研制的仪器在测量功率、电压、电流时的误差均小于0・01%。对多台实验样机的初步测试结果与上述理论分析和误差综合计算是一致的。
摘自:中国计量测控网







