首页>技术中心>技术资讯>神经网络技术在称重传感器中的应用研究
神经网络技术在称重传感器中的应用研究
发布时间:2017-09-01
1 引言
现代信息技术的三大基础是信息的采集、传输和处理技术,即传感技术、通信技术和计算机技术,它们分别构成了信息技术系统的“感官”、“神经”和 “大脑”。信息采集系统的首要部件是传感器,且置于系统的最前端。在一个现代自动检测系统中,如果没有传感器.就无法监测与控制表征生产过程中各个环节的 各种参量,也就无法实现自动控制。在现代技术中,传感器实际上是现代测试技术和自动化技术的基础。
在称重技术中,将重物放于称重系统的承载体上待稳定后,就可以准确地读出重量值。需要进行快速称重时,这种传感器就暴露出缺陷。由于其弹性体的 阻尼比较小,传感器到达稳态的时间较长,不能满足快速测量的要求。提高传感器动态响应的快速性,可从两方面入手。一是改变其结构、参数和设计。减少中间的 传递环节,提高传感器的固有频率,从而提高快速性;二是设计动态补偿器提高动态响应的快速性,即研制基于微处理器的数字动态补偿装置,串接在传感器之后, 以缩短整个测量系统到达稳态的时间。动态补偿器的设计要基于传感器的动态模型。另外通过神经网络技术提高传感器的性能。本文采用神经网络补偿方法,能自动 跟随传感器模型的变化,保证称重系统的快速性。同时给出解决这类问题的几种其他方案。
2 称重传感器的动态模型
称重传感器的动态模型如图 1 所示。图中,K 为弹簧刚度(N・m),C 为阻尼常数(N/m2),m0为传感器本身的等效质量,G 为被称重物的重量,B为基座,通常基座的质量很大,故认为它处于静止状态。因为重物与托架之间不是固定联接的,所以,需要两个方程来刻画上述的称重传感器 的动态特性。
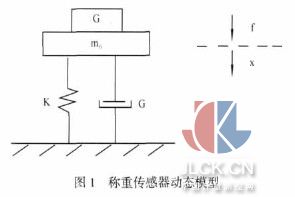
设 m 与 m0之间的作用力为 f,且假定两者之间无相对运动。
其阶跃响应如图 2 所示。动态过程振荡周期多,到达稳态的时间长,并且 m 值越大 Td越大,即达到稳定的时间越长。必须进行动态补偿,为适应被测重量的变化,需要神经网络自适应动态补偿。
3 神经网络补偿器的设计
若设计动态数字补偿器的传递函数是传感器传递函数的倒数,则整个测量系统的传递函数为 1,具有理想的频率响应特性。根据这一思想,我们设计一神经网络补偿器,使整个系统输出跟踪系统输入。
这种多网络自学习补偿结构是由两个结构和学习算法完全相同的神经网络 NN1,NN2 所构成。按误差 E=u- A 减少的方向调整连接权并使 u≈A。当网络收敛后,因网络 NN1 和 NN2 结构完全相同,所以有 y=u。
对应于 m=0.5kg,1.5kg 时的传递函数(8)式和(9)式,采用双线性变换
s=2(z- 1)/T(z+1),采样周期取 T=0.02 秒,得离散差分方程为:

采用三层网络,输入层有 5 个神经元,隐层有8 个神经元,输出层有 1 个神经元。采用 BP 算法,其主要思想是对于 q 个输入样本:P=[P1,P2,……Pq]已知与其对应的输出样本为 T=[t11,t2,……,tq]。学习的目的是用网络的实际输出 A=[a1,a2,……,aq]与目标矢量 t1,t2,……,tq之间的误差来修改其权值,使 a1,(l=1,2,……q)与期望的 t1尽可能地接近。隐层的激活函数为 f1,可调权值为W1ij,阈值为 b1i。输出层的激活函数为 f2,可调权值为 W2i。阈值为 b2i信息的正向传递。
因为在线学习是有一定时间限制的,而网络自身的学习也需要耗费一定的时间。如果直接将未训练的神经网络加入到系统中,当误差变化较大时,很可能 因网络自身学习的收敛速度跟不上误差的变化,而影响在线的学习效果。要克服直接在线学习的这个弱点,可以让网络在线学习之前进行离线训练。离线学习可以使 神经网络在系统工作之前预先完成自身的学习过程,以此获得一个基本反映系统要求的多层网络,使这个多层网络的参数基本工作在全局最小附近,然后再将这一网 络加入系统中去。在系统运行过程中,根据系统参数的实时变化,采用在线学习算法,让离线训练过的网络再随系统工作过程中参数的变化调整自身参数,从而能快 速、准确的辨识对象特性。这种离线学习与在线学习结合的方法,能很好的发挥各自的优势,大大提高了神经网络辨识系统的能力。还可以采用提高学习速率或采用 自适应速率来加以改进。在满足精度的前提下,应尽量减少结点数,提高训练速度。上述方法都有利于称重系统提高快速性和降低抖振。
神经网络 NN2 的结构与算法和 NN1 完全相同,略去。
采用随机初始化,取采样周期为 T=0.02 秒,训练矢量是 200 个,达到误差平方和小于 0.02 或最大循环次数为 5000 次。图 5 表示将训练好的神经网络加入系统中,当参考输入为:r(k)=0.5 或 r(k)=1.5 时系统的动态响应曲线。
补偿的动态过程对比图 2 可看出未加神经网络补偿的系统动态过程有近 100%的超调量,且动态调整时间长约 2 秒。加神经网络补偿后最大超调量小于 20%,动态调整时间缩短为只有 0.2 秒,且适合传感器参数变化的情况,该系统适合于快速测量。
自动控制以及计算机控制技术在解决称重传感器的动态性能方面有广阔的应用价值。实验仿真表明,自适应补偿也具有良好的效果。数字控制器设计中的 最少拍无差设计、最少拍无波纹设计在解决上述问题也有很大的优势,特别是最少拍和无波纹设计可以减小整个系统的超调量,具体的仿真结果我会在后续的文章中 提出。
4 遗传神经网络提高传感器性能的工作原理
下面以压阻式压力传感器为例,说明遗传神经网络在改善传感器性能中的应用。压阻式压力传感器受工作电流波动的影响,那么输出的电压值 U就是压力 P 和工作电流 I 的多元函数,即 U=f (P,)I。也可以认为压阻式压力传感器所测得的压力 P是电压 U 和工作电流 I 的多元函数,即 P=f (U,)I。要使神经网络有解决问题的能力,就要用大量的具有普遍性和代表性的学习样本训练网络,得到网络理想的权值,才能解决实际问题。所以首先要应对 压阻式压力传感器进行标定实验,以得到大范围内的学习样本和测试样本。
4.1 标定实验
标定实验的框图如图 6 所示,压阻式压力传感器的标准输入压力 P 由砝码产生,压阻式压力传感器的输入范围为 0.1~0.6MPa,可调电阻改变电路中的工作电流 I,压阻式压力传感器的输出电压经过调理电路和数采卡输入计算机,由Labwindows/CVI 编制的虚拟电压表读取电压值 U,由电流表读取电路工作电流值 I,由砝码读取标定压力值 P。
4.2 建立、计算数据样本
标定实验所得的标定数据如表 1 所示,工作电流从 3mA 变化到 7mA。可以看出,同一标定压力下,由于工作电流的影响,压阻式压力传感器的输出电压波动很大。
其中:α 为传感器系统输出电压相对波动率;max|ΔU|为最大绝对波动值;UFS为传感器系统满量程输出电压。
依照表 1 数据,max|ΔU|=4.7356-2.1048V,故 α=55%,由此可见该传感器的输出波动是相当大的。
将 0.1,0.3,0.5,0.6MPa 压力下的工作电流和传感器输出电压作为学习样本,标准压力值作为学习样本的期望输出。将 0.2 和 0.4MPa 压力下工作电流和传感器输出电压作为测试样本输入遗传神经网络进行计算,得到的测试样本网络输出如表 2所示。可以看出被测压力融合值的相对波动情况为:
其中:αP为传感器系统被测压力相对波动率;max|ΔP|为被测压力最大绝对波动值;PFS为传感器系统被测压力满量程值。
根据表 2 的数据得αp=5.7%,传感器系统的稳定性大大提高。
5 结论
提出了几种快速称重方法和提高传感器性能的原理,着重阐述了基于神经网络理论,设计出称重传感器神经网络动态补偿器和提高传感器性能。仿真研究 表明有效的提高了传感器动态响应的快速性,且对系统参数变化具有鲁棒性。将先进控制理论应用于实际传感器系统中,为提高传感器性能开辟了新途径,促进了称 重传感器行业的发展。
摘自:中国计量测控网







