液力变矩器三元流场计算的一种近似方法

发布时间：2017-09-01

1引言

液力变矩器的内部流动是极为复杂的三维流动。为了能够对其进行求解,采作两类相对流面的概念,并依此有了求解三元流动的普遍理论和方法。两类相对流面的基本思想是把叶轮内的三维流动问题,分解为两个分别沿着S1流面和S2流面的相关二维问题,两个流面相互迭代进行求解,直至满足精度要求。然而,在两类流面相互迭代求解的过程中,迭代求解的过程花费时间较长,还有可能出现求解不收敛的情况。于是本文提出了一种在两类相对流面基础上的液力变矩器三元流场计算的近似方法。该方法直观性强,无繁杂的迭代运算,计算程序容易编制,使用计算机内存少,计算时间短,且能满足一定的精度要求,适合于工程应用。

2基本假设

为了进行液力变矩器三元流场的近似计算,作出如下基本假设:

(1)液力变矩器叶轮内的流动是定常流动并且无空穴现象,工作介质是理想流体;

(2)液流沿着S1流面的运动是有势的;

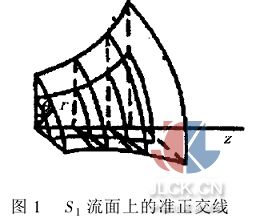
(3)流道中S1流面上的准正交线是S1流面上r和z均为常数的圆周线,即S1流面是回转面(见图1);

(4)平分叶片流道中流量的平均流面(即S2m流面)的形状与流面的几何中分面相近。

3计算的数学模型

有了以上基本假设以后,可得出求解的基本方程[1,2]:

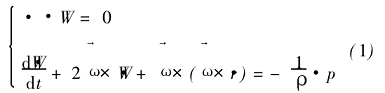
由基本方程(1)通过流线曲率法[4]、有限差分法[7]或有限元法[7]求出S2m流面上的流动参数分布。计算出S2m流面上的流动参数分布以后,用S2m流面上的流动参数求解流场中其他部分的流动参数。

在S_{1流面上的准正交线q =θ上的两点A和B的参数之间有如下关系:}

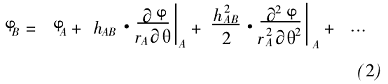
式中,φ―――空间点上的流动参数;

hAB―――点A和B之间沿θ的弧长;

rA―――点A的半径。

3.1z =常数时的计算方程式

在z =常数处,连续性方程为:

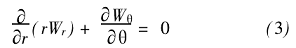
无旋条件为:

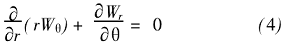
S_{1流面的方程为r= r(θ,z),该方程在z=常数时可写为}

S(r,θ) =0 (5)

于是可得

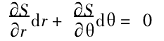
令

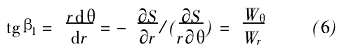
参数φ沿半径r的变化为

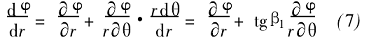
式(6)、(7)代入式(3)、(4)得

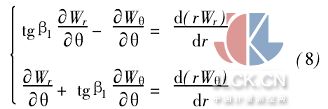
由式(8)得到一阶偏导数

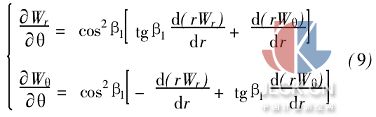
式(9)求导可得二阶偏导数

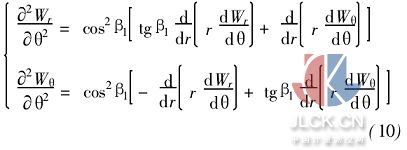
如有必要,可依此类推得到三阶、四阶等高阶偏导数。

3.2r =常数时的计算方程式

同理可得在r =常数处的一阶偏导数和二阶偏导数

如有必要,可依此类推得到三阶、四阶等高阶偏导数。

4计算步骤

(1)输入初始数据,划分流道中的计算网格;

(2)由基本方程求出S2m流面上的流动参数分布;

(3)计算出网格结点上的β1和β2的值;

(4)分别用式(9)、(10)、(11)、(12)计算出网格结点上z=常数和r =常数时的一阶、二阶偏导数的值,其中所用到的导数项通过三次样条插值函数[5,7]求出;

(5)用式(2)来求解S2m流面上任意一点A附近的zA= zB、rA= rB的B点流动参数。

5计算实例

现以YB355-2型液力变矩器为实例,计算其流场分布。已知参数:泵轮叶片数zB=26,循环圆半径R=0.16m,泵轮转速n =1200 rpm,泵轮与涡轮转速比I =0.7,泵轮入口相对速度W=5.16m/s。在泵轮流道中取7条准正交线(j=0,1,…,6)和5条流线(i =0,1,…,4)。

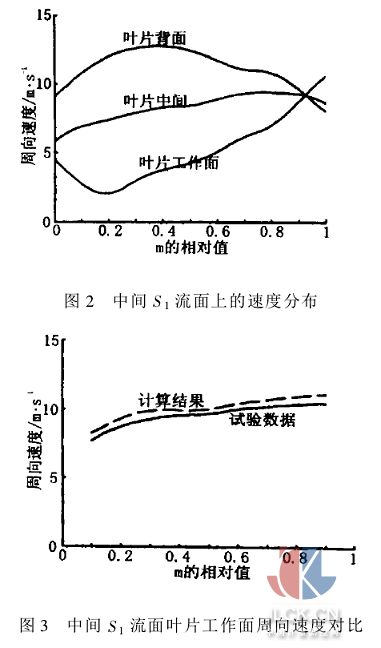
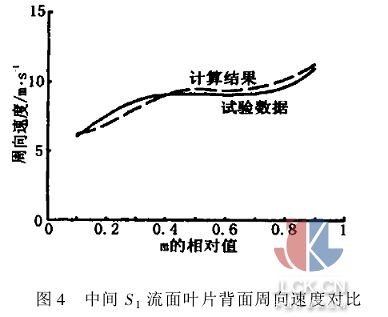
计算结果与试验数据[6]如图所示。图2为计算出的中间S1流面上的速度分布,图3、图4表示了中间S1流面叶片工作面、背面沿轴面流线方向周向速度的变化。

6结论

(1)通过本文可见,液力变矩器内三元流场计算方法的计算结果与实测结果基本吻合,满足精度要求,且计算过程中不需要迭代,简便实用。该方法可快速计算出沿周向叶片表面附近的流速及压力等流动参数的分布,适用于液力变矩器及其他透平机械内流场的实际计算。

(2)造成计算结果与实测结果存在微小差异的原因,主要是在计算过程中进行了大量的数值微分运算,由此降低了该方法的计算精度所致。但是在一定精度要求的范围内,并不影响该方法的应用。

摘自：中国计量测控网

本文由乔科化学&云试剂商城整理编辑，如有侵权请联系删除