支撑面积对薄镜面形影响的研究
发布时间:2017-09-01
引言
随着空间光学系统和高功率激光系统向大口径方向发展[1],系统主要光学元件的口径不断增大, 这极大地影响了整个光学系统的质量和体积,以及工程的成本。因此,通过减小元件厚度,使用薄型和超薄型光学元件来改善系统结构成为目前光学系统设计的主要方式[2]。但随着光学元件厚度的降低,直径厚度比的增大, 元件面形在使用过程中非常容易受到外界因素的影响(如重力作用、机械振动),导致光束质量的恶化,其中,镜面的自身质量和支撑结构产生的镜面变形尤为突出。考虑到镜面支撑结构中轴向支撑比径向支撑对镜面变形的作用更大,因此,必须设计一套合理的支撑结构来尽可能地降低镜面自重产生的变形,从而获得较好的表面面形。另外,由于天文望远镜主镜与高功率激光系统中的大口径反射镜在应用上的不同,它们对不同空间频率范围的面形畸变控制要求不一样[3],因此,在设计支撑结构时,还必须考虑镜面变形的空间频率特性。基于此,利用有限元法对薄型镜面变形情况进行分析,然后通过设计不同的支撑单元面积,分析元件面形变化, 最后分别从空间域与频率域上分析了支撑单元大小对镜面形状的影响。
1 基本理论
由于可以将各种晶体或玻璃材料生产的光学元件看作弹性体,这样在分析其变形过程时,可以利用弹性力学中的薄板弯曲小挠度方程荦2荦2 w=q/D 进行求解[4]。而该方程只有在环带支撑情况下才具有解析解,对目前广泛使用的多点支撑方案得不到解析结果,所以文中选择有限元法来求解。
有限元法的基本思想是将连续体划分为有限个在节点处连接的小单元,然后利用在各单元内假设的近似函数来分片逼近全求解域上的未知场函数。文中将二维圆板离散成若干个矩形单元,每一单元的模型如图1 所示。图中矩形单元两边长分别为2a和2b,有4 个节点(i、j、m、p),每个节点有3 个自由度( 沿z 轴方向的挠度w、绕x 轴的转角θ x 、绕y 轴的转角θy )。由于只受到沿z 轴方向重力的作用,利用最小位能原理建立有限元方程Ke ae =Pe [5],将矩形板单元中节点的位移表示成单位刚度矩阵与等效节点载荷的乘积。
E 为弹性模量;t 为矩形单元厚度;μ 为泊松比;ρ 为单元单位厚度的质量,即载荷。因此,将公式(2)带入公式(1),再加上固支边界条件,就可得到矩形单元节点的位移,然后推广到整个模型,得到模型的挠度w,就可以计算模型各点的应力、P蛳V 和RMS 值等,为研究面形的变化做准备。
2 有限元模型计算结果及分析
以K9 玻璃为镜面材料,具体参数:弹性模量E=81.32 GPa,泊松比μ=0.209,密度ρ=2.53 g/cm3。光学元件口径Φ200 mm,厚度h=10 mm。将其进行有限单元划分后。
2.1 支撑单元面积对元件面形影响的空域分析
在光学元件上施加9 个支撑单元, 如图3 所示。内环3 个支撑单元,距圆心25 mm,外环6 个支撑单元,距圆心70 mm,沿圆周均匀分布。在具体计算时对9 个支撑单元均施加全约束,首先固定内环3 个支撑单元的面积均为28.756 mm2,改变外环支撑单元的面积, 分析外环支撑单元大小对元件面形的具体影响;然后在固定外环6 个支撑单元的面积均为555.146 mm2,改变内环支撑单元的面积,分析内环支撑单元大小对元件面形的具体影响。图4 为外环支撑单元面积变化得到的图形。(a)、(b)、(c)的外环支撑单元平均面积分别为8.827 mm2、158.324 mm2、555.146 mm2。在有限元分析过程中,面积的计算由所划分的有限单元大小决定, 考虑支撑单元面积的相对误差在5%的合理范围内,得到如下数据,如表1 和表2 所示。可以看出:相对于外环支撑单元面积,内环支撑单元面积的变化对面形的P蛳V、RMS 值的影响不大, 内环支撑单元面积从0.8940 mm2 增大到28.756 mm2, 其P蛳V 和RMS值分别变化了0.5%和9%。因此,文中主要研究外环支撑单元面积的变化对面形影响。
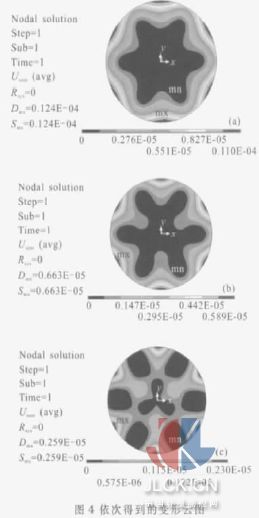
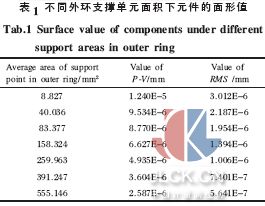
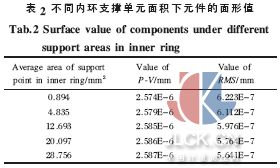
为了进一步分析外环支撑单元面积变化对面形的影响,通过图5 和图6 可以进行直观的研究。
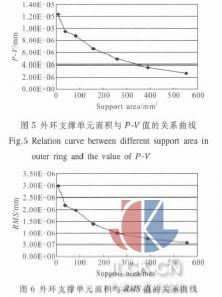
由图5 和图6 可以看出:随着外环支撑单元面积的增大,镜面的变形在减小,其P蛳V、RMS 值逐渐减小,当外环支撑单元面积由8.827 6 mm2 增大到555.146 mm2后,其P蛳V、RMS 值下降了大约80%。计算结果说明:外环支撑单元面积大小对空间域下的镜面变形有明显作用,通过增大外环支撑单元面积可以获得较好的面形,这对于以后的工程设计有重要的参考意义。
2.2 支撑单元面积对元件面形影响的频域分析
在高功率激光系统应用中,非常关注光学元件面形畸变在频率域中的分布[3],利用一维PSD 曲线来具体分析支撑单元面积变化对元件面形畸变在频率域中的影响。由图4 可知:元件面形畸变具有对称性,一维PSD 曲线可以较好地反映整个面变形情况的频域信息。在计算中使用一维模型,如图7 所示。
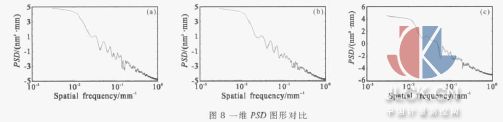
在模型中L=200 mm,H=10 mm,W=10 mm, 共401 个节点。设定在两端简支, 在1 和2 处的支撑单元施加固定约束,当支撑单元大小变化后,计算得到的PSD 曲线如图8 所示,(a)、(b)、(c)在1 和2 处的支撑单元大小分别为5、7、13 mm。
从图8(a) 可以看出: 此时由PSD 曲线反映出元件主要面形误差分布在空间频率大约为0.17 mm-1处。当支撑单元逐渐增大到7 mm 时,面形误差的频率分布没有明显变化,但是图8(b)中显示的突变值幅值在减小,也就是该频段误差值降低。继续增大对称支撑单元的长度,从图8(c)可以看出:主要误差频率由0.17 mm-1 移向了0.2 mm-1,元件面形误差已经进入了中频段[7]。计算结果说明支撑单元的大小对波前误差的空间频率分布有明显的影响,当支撑单元面积略微增大时,相当于减小了调制深度[8], 其突变值的幅度将减小;当支撑单元面积增大较多时,又相当于增加了调制频率[8],其突变值的位置将向较高频段移动。
3 结论
分析了薄型镜面在多点支撑下,设计不同支撑单元面积而产生的镜面变形情况, 通过计算P蛳V、RMS值得知:从空域分析来看,支撑单元面积与光学元件面型之间的关系是增大外环支撑单元的面积可以明显减小P蛳V、RMS 值而获得较好的面形; 从频域分析的结果来看,支撑单元面积增大将使元件面形误差向较高的空间频段移动,甚至可以达到中频段。对于空间成像系统而言,影响成像质量的主要是元件面形畸变的低频段部分,而对于高功率激光系统而言,中频段畸变信息将导致明显的非线性破坏,因此,针对不同的应用应该合理考虑支撑单元大小的影响。经过初步分析可知,采用多点支撑方案进行大口径光学元件的支撑时,如果在大口径望远系统中,可以尽量增大支撑单元的面积;而在高功率激光系统中,则不能使用过大的支撑面积,以免增加中频段误差。
摘自:中国计量测控网







