首页>技术中心>技术资讯>基于衍射理论的分块镜共相位误差的高精度测量
基于衍射理论的分块镜共相位误差的高精度测量
发布时间:2017-09-01
引言
大型望远镜是物理学家及天文学家研究宇宙起源最重要的工具,望远镜的集光能力及角分辨率随着口径的增大而增强,集光能力越强,就能看到越暗越远的天体,即能够看到更早期的宇宙,天体物理的发展需要更大口径的望远镜。从16 世纪伽利略发明望远镜到当今美国加州理工大学建造的10 m 口径的凯克望远镜,主镜口径在不断增大。但是,随着望远镜口径的增大,一系列的技术问题接踵而来。首先,望远镜的自重引起的镜头变形影响相当大,镜面畸变严重影响成像质量[1]。其次,从制造成本来看,传统方法制造望远镜的费用几乎与口径的平方甚至立方成正比[2],因此,从20 世纪80 年代开始,采用可收展式的分块镜的思想逐步发展起来[3],如图1 所示。
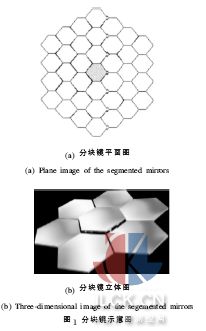
拼接式分块镜光学系统能满足下一代太空望远镜更大、更轻和可折叠的要求[4]。拼接镜面即将一系列子镜拼接在一起达到单一镜面的光学性能。如果不采用分块镜共相位成像技术,整个光学系统的分辨力将受限于单个分块镜的分辨力,分块镜共相位误差的存在会严重影响成像质量。分块镜光学共相位误差与系统成像质量之间存在如下关系[5]: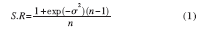
式中: S.R 为斯特列尔比, 是光学系统像质评价的一种指标, 理想值为1;σ =2kδ = 4πλ δ ,λ 为波长,δ 为各分块镜镜面之间高度差的均方根值;n 是分块主镜的数量。要保证系统具有优良的像质,各分块镜之间高度差的均方根值要达到δ≤λ/20。沿光轴方向,分块镜之间的高度差即为共相位误差,如图1 (b)所示。分块镜在展开后首先进行机械调整,将误差范围尽量减少,然后进入合像环节, 将倾斜等量检测并校正到很小的范围内,满足共相位误差的检测要求。对于尺度为米级的大型分块镜而言, 要把各分块镜之间的共相位误差检测到λ/20 的精度水平, 是一个极具挑战性的难题。因此, 分块镜共相位误差高精度的检测和校正是实现超大口径、甚高分辨率成像的前提和技术关键。
分块镜共相位误差的检测通常采用分步测量的方法,用宽光谱光源进行粗测,将共相位误差的测量范围减少到一个波长范围内。切换单色光光源,利用单色光实现纳米级的高精度测量。美国在这方面的研究处于领先地位,Keck 地基天文望远镜用PSF 法[6]实现共相位误差的测量,该方法系统结构简单,但是计算量较大,测量周期长。美国加州大学的Gary Chanan等人发展了一种新的基于相位反演原理的分块镜共相位误差检测方法, 即相位反演法(PDS)[7]。目前,NASA 正在着手第二代太空望远镜(NGST)的研制,提出了色散条纹法(DFS)[8]。这两种方法的测量精度较高,但是系统较前者更为复杂,不利于空间环境下的高精度测量。我国在这方面的研究起步较晚,中国科学院光电技术研究所采用基于迈克尔逊干涉系统的拼接主镜的共相位误差检测技术[9-11],该方法系统复杂,对噪声较为敏感,很难适应空间环境下的高精度测量。
文中研究相邻分块镜之间的共相位误差检测,衍射光斑的峰值位置偏离中心位置的距离随共相位误差的变化规律,利用该理论实现一个周期范围内共相位误差的高精度测量,并进行了实验验证。该方法系统结构简单,所需像斑的采样点少,有利于空间环境下的共相位误差检测。
1 检测原理
1.1 共相位误差测量原理
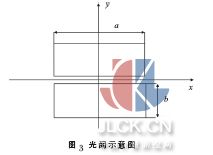
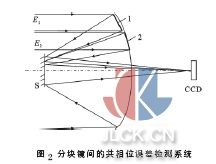
相邻分块镜之间共相位误差检测系统如图2 所示,E1和E2为入射平行光,1 和2 为反射镜,1 和2 的连接处设置了方形光阑, 横跨相邻两个分块镜,S 为次级反射镜。入射光经过光阑及反射镜在焦面发生衍射-干涉,采用CCD 可以接收到衍射-干涉图。图3为方形光阑示意图。其中a,b 分别为光阑的长和宽。当分块镜1 和2 之间存在共相位误差,E1和E2经过反射镜后存在光程差, 衍射光斑也会随共相位误差的变化而变化。入瞳函数为:
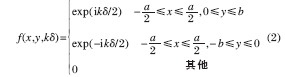
根据波动光学及傅里叶光学理论, 焦面处衍射-干涉图的一维光强分布为: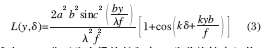
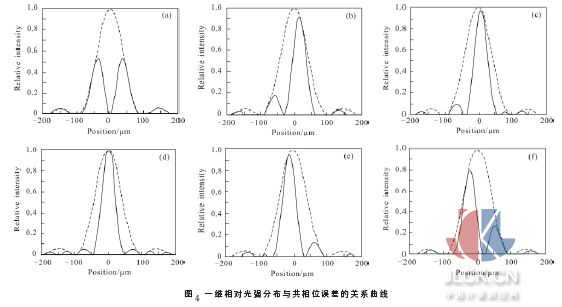
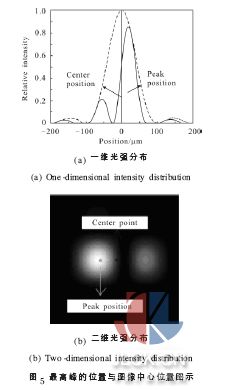
式中:a, b 分别为光阑的长和宽;δ 为分块镜之间的共相位误差;k=2π/λ 。衍射-干涉图随共相位误差的变化而变化,如图4 所示,图中,(a)~(f)是共相位误差分别为-0.5λ ,-0.25λ ,-0.1λ ,0,0.15λ ,0.3λ 所对应的一维衍射-干涉图, 虚线为包络曲线, 横轴为位置坐标,纵轴为相对光强。衍射-干涉图随共相位误差的改变而明显不同。以图像中心为参考点,最高峰的峰值位置随共相位误差的变化而移动。图5 为最高峰的峰值位置与图像中心位置。共相位误差为零时,最高峰位于图像中心,随共相位误差的增大,最高峰上移(对应y 平面为左移)。共相位误差为负时,最高峰位于图像中心下侧(对应y 平面为右移)。
1.2 最高峰位置与共相位误差的关系
由公式(3)可知:衍射-干涉图的光强分布是sinc函数和余弦函数的乘积,最高峰的峰值位置是该函数L(y,δ )的拐点位置。对函数L(y,δ )求导数,导数为零的点即为拐点,但是,该函数的导数没有准确的解析表达式,需要对该表达式进行分析,得到零点位置。对公式(3)中的sinc 函数的平方在y=0 附近进行泰勒展开:
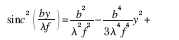

令L(y,δ )的一阶导数为零,计算拐点位置。由于共相位误差是10-7 量级,δ 的高次幂可以忽略, 经过理论推导得到最高峰的位置与共相位误差δ 的关系为: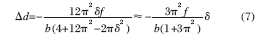
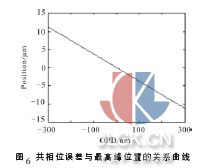
共相位误差与最高峰位置之间近似为线性关系,仿真曲线如图6 所示。横轴为光程差,纵轴为最高峰相对于图像中心的位置。共相位误差为负,最高峰处于图像中心的左侧,随着共相位误差逐渐变小,最高峰位置逐渐右移。共相位误差为零时,最高峰相对于图像中心的距离为零。
1.3 峰值位置的确定
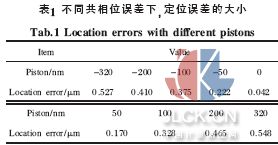
最高峰峰值位置的确定直接影响测量精度。根据共相位误差与峰值位置的关系,可以确定采用可见光光源,如要满足λ /20 的测量精度,最高峰的定位误差需要控制在800 nm 的范围内, 采用基于高斯拟合的峰值定位方法来确定最高峰的峰值位置。在光阑为 1 cm、焦距为0.5 m 的情况下,亮斑大约为60 μm。根据公式(8)计算图像的质心:
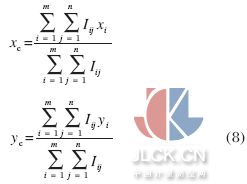
在质心附近判断最高峰的位置,然后设置阈值,提取最高峰。
在峰值两侧取点作高斯拟合。假设高斯拟合曲线表达式为:

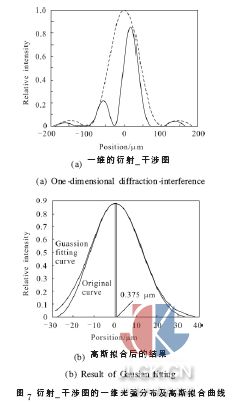
式中:m 为未知数个数;n 为采样点个数。在像元尺寸为5 μm、采样点为10 个左右的情况下,该峰值定位方法的定位误差小于600 nm,如表1所示,能够满足所要求的定位精度。图7(a)为一维光强分布图, (b)为在峰值左右取10 个点拟合得到的高斯曲线, 其峰值位置与原曲线的峰值位置误差为0.180 μm。分析光阑的衍射-干涉图的光强分布可以得出:在共相位误差为零时,像斑中心为一个大的主峰,两侧有小的侧峰,并且图像中心对称。随共相位误差的增大,像斑主峰逐渐变小,侧峰逐渐变大,主峰的对称性逐渐变差,当这两个峰一样大即共相位误差达到半波长时, 主峰的对称性最差,但是定位误差仍然在允许范围内。
2 实验
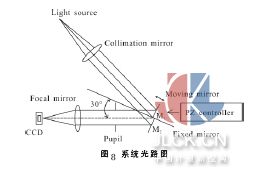
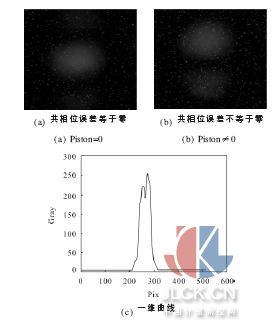
实验采用单色性强的He-Ne 激光器作为光源,光源发出的光经过准直透镜,得到平行光,再经过分块镜M1和M2,以及1 cm 的方形光阑,发生衍射-干涉,通过会聚透镜得到衍射光斑, 采用CCD 接收衍射光斑图像。M1和M2是从同一块平面度很好的镜子上切割下来的, 其中,M1为动镜,M2为定镜, 通过压电陶瓷控制器来控制动镜。会聚透镜焦距为0.8 m。CCD像元尺寸为4.65 μm×4.65 μm,系统光路图如图8所示。用压电陶瓷控制M1, 将M1和M2之间共相位误差调为零,得到图9(a),计算图像的中心位置,零共相位误差时,衍射光斑具有中心对称性,光斑的质心位置与中心位置重合,图像的质心即为中心位置,以此作为参考点。图像是关于纵轴对称的,图像中心横坐标与质心横坐标相同,不随共相位误差的变化而变化。
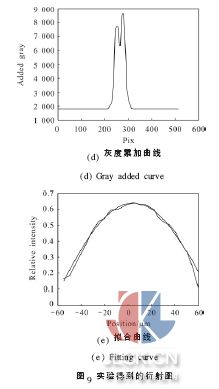
压电陶瓷制动器控制动镜,改变共相位误差的大小,得到的衍射光斑如图9(b) 所示, 其y 平面的灰度曲线如图9(c)所示,纵轴为灰度值,横轴为位置坐标。由于衍射图像质心所在的纵轴对称,图像灰度进行横向叠加后,中心位置坐标不变,而且灰度累加可以减少随机噪声的影响,减少定位误差。所得到的纵向灰度曲线如图9(d)所示,纵轴为灰度累加, 横轴为位置坐标,利用上述的高斯拟合曲线确定衍射光斑最高峰相对于图像中心的距离为14.393 μm, 如图9 (e)所示。经过计算共相位误差为93 nm。压电陶瓷的位移量为65 nm, 即共相位误差值为65 nm, 测量误差为28 nm。由于实际实验条件的限制,受噪声及压电陶瓷精度影响,误差较大,但仍能满足λ /20 的测量精度,该方法能够有效检测分块镜共相位误差。
3 结论
通过以上分析可以得出如下结论:
(1) 一个波长周期范围内, 衍射光斑最高峰的峰值位置偏离图像中心的距离与共相位误差之间呈线性关系。采用可见光光源,要达到λ/20 的精度,峰值定位精度要优于800 nm。
(2) 基于高斯拟合的峰值定位方法的定位误差小于600 nm,满足定位要求,计算简单, 适合该测量方法。且CCD 像元尺寸越小,定位精度越高。
(3) 利用衍射光斑的峰值位置判断共相位误差的方法是一种有效的测量方法,由于实验条件限制,振动及噪声对衍射光斑有一定影响,使得误差稍大,但实验结果表明:该方法的测量精度能达到λ /20。
摘自:中国计量测控网







