双筒式减振器的热力学模型
发布时间:2017-09-01
目前,车辆上广泛应用的双筒式液压减振器工艺简单、成本低廉,但散热困难。因为它主要通过阻尼阀对油液节流产生阻尼力衰减车身振动,所消耗掉的振动能量将转换成为热能,使缸体温度不断升高。当缸体温度达到并超过密封件所能承受的极限温度后很容易导致油液的泄漏。虽然减振装置的散热能力对系统可靠性影响很大,但由于涉及不少跨学科专业知识,所以国内还没有展开相关的研究工作,国外公开出版的文献也甚少。基于这种情况,本文对双筒式减振器的热力学模型进行了系统研究。
1热力学物理模型
建立的双筒式液压减振器热力学物理模型如图1所示。将两只缸筒套装在一起,在内筒中形成了减振器的工作室,内外筒之间为储油腔,用来储存和补偿工作室中的油液;储油腔中通常充有一定压力的空气,按照常规设计,可设其中油液占储油腔容积的一半;活塞杆下端装有活塞,在内筒中起支承和导向作用,并将工作室隔离为上下两腔;活塞上安装有压缩和复原阀,通过对油液节流产生阻尼力衰减车身的振动;底阀将下腔与储油腔隔离开,具有泄流及向工作室补充油液的作用,以防止减振器出现空程性畸变。
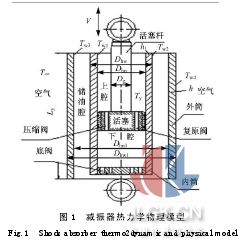
图1中,Dhw为内筒外径;Dhw1为外筒外径;Dhn为内筒内径;Dhn1为外筒内径;Dg为活塞杆直径;Ty为油液温度;Tw1为内筒内壁温度;Tw2为内筒外壁温度;Tw3为外筒内壁温度;Tw4为外筒外壁温度;h为外筒壁厚;h1为内筒壁厚;T∞为外界环境温度;V为活塞杆运动速度;Ly为缸筒长。
2热力学数学模型
2.1生热机理
如图1所示,在工作过程中双筒式减振器阻尼力所消耗的振动能量被用来增加油液分子的热力学能,宏观上表现为油液温度的升高,其能量的传递关系为:在初始时刻,缸内温度与环境温度相同。压缩行程时,下腔部分油液通过活塞上的压缩阀进入上腔,以补充其增大的容积;另一部分油液则通过底阀进入储油腔。在油液流过阻尼阀时,由于速度很快,流体与外界的热量交换通常很少,但在阻尼阀附近会产生涡流、扰动(流体的内摩擦)等现象,所以节流是典型的存在内摩擦的绝热流动过程。理论上讲,流过阻尼阀的油液所产生的动能与增加的热力学能之和同压缩阻尼力做的功是守恒的,当下腔油液通过阀组分别进入上腔和储油腔后,将与两腔中的油液混合并发生热力学能的变化;复原行程时,上腔油液通过活塞上的复原阀进入下腔,而储油腔中的部分油液通过底阀也进入下腔以补充其增大的容积。同理,流过阻尼阀的油液所产生的动能与增加的热力学能之和同复原阻尼力做的功是守恒的。当这两部分油液进入下腔后,会导致油液热力学能的再次变化,就这样周而复始,最终油液温度不断升高。
2.2数学模型
减振器的热量传递方式通常以热传导和热对流为主。热传导又简称导热,它是指热量由物体的高温部分向低温部分的传递,或者由一个高温物体向与其接触的低温物体的传递。当缸筒内外壁温度不同时,就会在固体内部产生导热现象。柱坐标系的导热微分方程[1]为
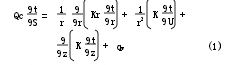
式中:ρ为缸体密度;c为缸体材料比热容;λ为缸体材料导热系数;qv为内热源发热率;t为摄氏温度;τ为热量传递的时间。
在减振器的工作温度范围内,缸体材料一旦确定,其导热系数可设为常量,无内热源时有qv=0;另外,缸体导热的温度场属沿轴线对称分布的一维导热,所以式(1)可简化为
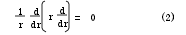
根据导热微分方程和傅立叶定律联合推导可分别得出内、外筒壁的导热方程式
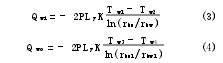
式中:Qwi、Qwo分别为内、外筒壁所传递的热量。
在储油腔中,设上半部分为带有压力的空气,下半部分为油液。由于减振器工作时通常液面不会剧烈波动,所以储油腔中的介质也主要以热传导的方式向外界散发热量,根据式(2)及傅立叶定律可分别推导出空气与油液的导热方程式
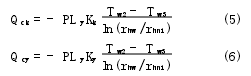
式中:λk为空气的导热系数;λy为油液的导热系数;Qck为储油腔中空气所传递的热量;Qcy为储油腔中油液所传递的热量。
联立式(3)~式(6)并根据热量传递关系整理得出热传导的综合表达式为
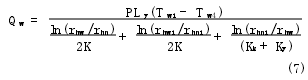
工程上遇到的大部分问题往往不是单纯的热对流方式,而是当流体流过不同温度的固体表面时,依靠热传导和热对流联合作用的热量传递过程,称为对流换热过程。减振器中工作室油液与内筒之间,外筒与环境之间的热量传递都属于对流换热。
由传热学理论可知,空气在外筒近壁处边界层的发展不因空间限制而受到干扰,属于大空间自然对流换热。通过邱吉尔(S.W.Churchill)所提出的计算关联式[2],可以推导出竖直状态缸筒外表面换热系数的表达式为
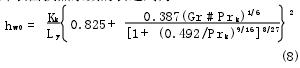
式中:格拉晓夫数为Gr =gβ(Tw4-T∞)L3yv2k;普朗特数为Prk=vkλkρkck,其中ck为空气的比热容;ρk为空气密度;vk为空气的运动黏度;β=1V
��Tp为容积膨胀系数,亦称体膨胀系数。工作室油液与内筒之间属于管内强迫对流换热[3]。由凯斯推荐的努赛尔数特征关联式[4-5]可推导出层流状态下内筒内表面的强迫对流换热系数为
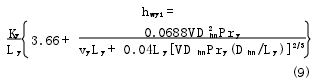
紊流状态下内筒内表面的强迫对流换热系数为

由式(7)和牛顿冷却公式可推导油液散发到外界环境的热量综合表达式为
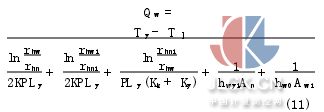
式中:Ahn为内筒内表面积;Aw1为外筒外表面积。以油液作为研究对象,根据能量守恒原理进行推导有
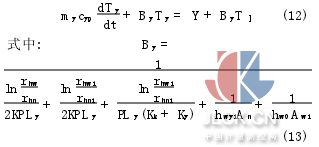
阻尼阀按小孔和缝隙节流计算,则有
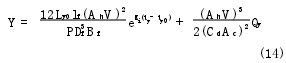
式中:my为油液质量;cyp为油液的定压比热容;ρy为油液密度;Ac为节流孔面积;流量系数Cd=0.62;δf为缝隙的宽度;Bf为缝隙的湿周;lf为缝隙的长度;μy0为油液的初始动力黏度;λi为油液的黏温指数;Ah为活塞有效工作面积。联立式(3)~式(13)即组成了双筒式减振器的热力学数学模型。
若将减振器外筒壁喷涂成黑色,则还需考虑热辐射的换热量。热辐射换热量的表达式[6]为
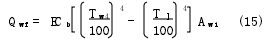
式中:黑体辐射系数Cb=5.67 W/(m2・K4);ε为热辐射发射率。
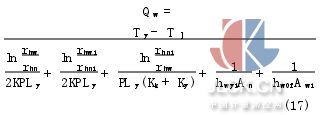
推导外筒外壁的复合传热系数表达式为
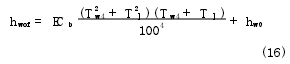
将式(16)与式(7)和牛顿冷却公式联合整理得出考虑热辐射时油液散发到外界的综合热量表达式为
式(13)也改为
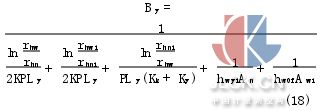
联立上述所推导的各项表达式即组成了考虑热辐射的双筒式减振器热力学数学模型。
2.3模型仿真分析
通过数学软件Matlab编程对减振器的热力学模型进行迭代运算。相关参数如下:δf=0.1×10-3m,Bf=0.25 m,Cd=0.62,lf=1×10-3m,λ=23 W/(m・K),T∞=300 K,ρy=890 kg/m3,λt=0.02,ρ0=1.293 kg/m3,T0=273 K,μy0=8.9×10-3kg/(m・s),节流小孔面积取为Ac=1×10-4m2。系统的初始温度与外界环境温度相等,激励为振幅A=0.05 m的正弦曲线,频率取为f=1 Hz。为便于分析,设减振器每工作一个循环,就与外界交换一次能量,循环次数X=5000,单次循环时间t=1/f。
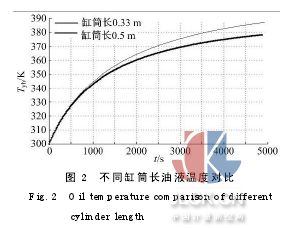
(1)设定减振器的基本结构尺寸为:Dhn=0.065 m,Dhw=0.07 m,Dhw1=0.09 m,Dhn1=0.085 m,Dg=0.026 m,Ly为0.33 m和0.5 m,仿真结果如图2所示。
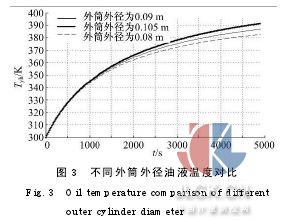
(2)设减振器的基本结构尺寸为:Dhw=0.07m,Dhn=0.065 m,Ly=0.33 m,Dg=0.026 m,Dhw1取为0.08、0.09、0.105 m,Dhn1取为0.075、0.085、0.1 m,仿真结果如图3所示。
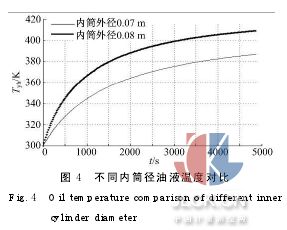
(3)设减振器的基本结构尺寸为:Dhw1=0.09m,Dhn1=0.085 m,Dg=0.026 m,Ly=0.33 m,Dhw取为0.07、0.08 m,Dhn取为0.065、0.075 m,仿真结果如图4所示。
(4)设减振器的基本结构尺寸为:Dhw=0.07m,Dhn=0.065 m,Dhw1=0.09 m,Dhn1=0.085m,Ly=0.33 m,Dg为0.02 m、0.026 m,仿真结果如图5所示。
由图2可以看出,减振器其他参数确定后,筒长为0.33 m时,循环末端油液温度为387 K;当筒长为0.5 m时,循环末端油液温度为378 K。即随着缸筒长度的增大,油液在相同时间内的温升逐渐减小。
由图3可以看出,在减振器缸筒壁厚及其余参数确定后,当外筒外径为0.08 m,内径为0.075m时,循环末端油液温度为383 K;当外筒外径为0.09 m,内径为0.085 m时,循环末端油液温度为387 K;当外筒外径为0.105 m,内径为0.1 m时,循环末端油液温度为392 K。即随着减振器外筒径向尺寸的增大,油液在相同时间内的温升逐渐增大。
由图4可以看出,在减振器缸筒壁厚及其余参数确定后,当内筒外径为0.07 m,内径为0.065m时,循环末端油液温度为387 K;当内筒外径为0.08 m,内径为0.075 m时,循环末端油液温度为409 K。即随着内筒径向尺寸的增大,油液在相同时间内的温升逐渐增大。
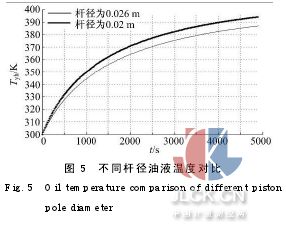
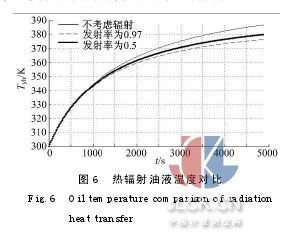
由图5可以看出,在减振器其他参数确定后,当活塞杆直径为0.02 m时,循环末端油液温度为394 K;活塞杆直径为0.026 m时,循环末端油液温度为387 K。即随着活塞杆径向尺寸的增大,油液在相同时间内的温升逐渐减小。图6为热辐射油液温度的对比图。由图6可以看出,不考虑热辐射时,循环末端减振器油液温度为387 K;在把外筒壁面喷涂成深色后,发射率逐渐增大,这时就需要考虑热辐射的换热量。当发射率为0.5时,循环末端油液温度为380 K;当发射率为0.97时,类似于黑体辐射,循环末端油液温度为377 K。即随着缸体发射率的增大,油液温度在相同时间内的温升逐渐减小。
通过上述分析可知,在阻尼阀结构尺寸不变的情况下,随着缸筒轴向尺寸以及活塞杆径向尺寸的增大,相同时间内减振器油液温升逐渐减小;随着内外缸筒径向尺寸的增大,相同时间内减振器油液温升逐渐增大;当减振器外表面喷涂深色或黑色漆后,随着表面热辐射发射率的增大,相同时间内减振器油液温升逐渐减小。
另外,由以上各图可以看出,随着时间的增加,油液温度逐渐趋于稳定,这是因为阻尼阀节流所产生的阻尼力与油液黏度有关。油液温度上升,分子运动加剧,黏度迅速降低,阻尼力不断减小,所消耗的振动能量以及转换的热量也减少,而随着缸体温度的升高,系统与外界环境温差越来越大,散热量不断加大,所以系统最终将达到一个温度的平衡点。
3结论
(1)阻尼阀结构参数不变时,增大缸筒轴向尺寸以及活塞杆的径向尺寸,或者减小内外缸筒的径向尺寸,都能够使减振器油液温升降低。
(2)为了增加系统散热量,可在减振器外表面喷涂深色或黑色漆,提高热辐射发射率,从而有效减缓油液的温升速度。
(3)随着时间的推移,系统将达到温度平衡点,通过调整减振器的相关参数,将平衡点控制在密封件极限温度范围内,这样可以避免泄漏。
摘自:中国计量测控网







