快速响应反射镜主动减振技术
发布时间:2017-09-01
引言
光学系统是一种较为精密、复杂的系统,通常工作在相对稳定的实验室环境中。随着光学系统应用领域的不断扩展, 一些复杂的光学系统逐渐从实验室走向实际应用现场, 而大部分应用现场的环境相对于实验室要恶劣得多, 在应用现场进行的光束传输实验, 不可避免地存在着附属设备的随机振动和地面的抖动, 严重影响光束的质量及光束指向的稳定性。因此,研究光学系统的减振技术,对提高光学系统的工作稳定性具有重要的意义[1]。
由于振动干扰的复杂性, 传统的无源隔振技术很难有效地隔离精密设备工作平台的超低频振动信号,因为无源隔振元件( 如隔振器等) 的刚度不可能无限降低,隔振器参数也不能实时调节。与此同时,有源隔振系统在隔离超低频振动方面相比无源要成效显著些。但是工程实用化都还有一定的距离。为了达到理想的减振效果, 文中将有源控制和光路计算相结合,基于几何光学、机械控制和减振隔振理论[2-7],研究提出了一种基于快速响应反射镜的主动减振技术,有望应用到实际的减振控制中。
1 基于快速响应反射镜的主动减振技术
1.1 技术原理
文中提出的基于快速响应反射镜的主动减振技术原理是依据传输光线失调方程, 得出光路失调量与光路中快速响应反射镜位姿之间的计算关系[8-11],从而获取反射镜所需作动的角度值, 利用步进电机调节反射镜,补偿振动引起的光路失调,达到光路稳定的目的,原理如图1 所示。入射光路经快速响应反射镜反射后,经分束镜一路出射,一路作为探测光路进入接收屏,同时采用CCD 及其数据采集系统对探测光路进行检测。

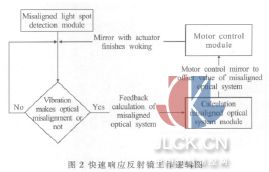
所谓的快速响应反射镜就是装有作动器的反射镜, 可以根据振动引起的光路失调量计算其作动响应值,通过步进电机控制其位姿。其中,快速响应反射镜工作逻辑如图2 所示。首先由光斑失调检测模块对探测器获取的光斑进行实时检测, 从而得到光斑失调量[12];考虑实验搭建的光路,具有图象背景灰度值较小、目标灰度值较高、且目标的灰度分布为抛物面或高斯曲面等特性, 因此采用灰度重心法来定位光斑[13-18];然后通过光路失调计算模块对光斑失调量进行计算,并得出快速响应反射镜补偿量;最后由快速调节反射镜电机控制模块对反射镜进行调节, 通过反射镜的快速调整来补偿由于振动引起的光路失调,最终使光路达到稳定[19-20]。
1.2 数值计算
基于几何光学及矩阵光学理论[21], 分析光学系统的振动失调光束传输变换矩阵, 根据机械振动引起的近轴光学系统的光束指向在三维位移失调下的传输方程, 找出光路失调量与光路中快速响应反射镜位姿之间的计算关系。
文中以反射镜面法线方向为z 轴方向, 镜面为xoy 面,反射镜的6 个自由度沿着x、y 轴方向的移动和绕着z 轴方向的转动对反射镜出射光线方向并无影响。
下面进一步研究沿z 轴方向的移动和绕x、y 轴方向的转动量对接收屏上光斑位置的影响。其中反射镜入射角为α ,δi为线位移,εi为角位移,p 表示入射光线,q 表示扰动光线,扰动光线在反射镜面的法向线位移为δnq, 入射光线初始状态下在x、y 轴线位移的分量δxp、δyp, 转动的角位移在镜片平面内的分量为εy,反射面内的切内角位移分量为εx。计算反射镜沿z 轴移动后的光线传输失调量。如图3 所示, 可得反射镜沿z 轴扰动δn引起的接收屏上光斑位置的失调量为:
kzn=(δnq/cosα)cos(π/2-2α)=2δnqsinα (1)
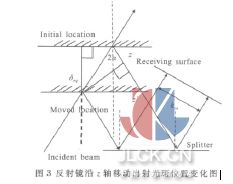
计算反射镜绕z 轴左右、上下转动后的光线传输失调量, 即绕x、y 轴方向的转动引起光线传输失调量。如图4 所示,反射镜分别绕x、y 轴方向转动ε 后传输(l1+l2)距离,εxq表示扰动光线在反射镜面内的切内角位移分量,εyq表示扰动光线在镜片平面内的位移分量,光斑位置在接收屏水平x、垂直y 方向上的失调量分别为klx、kly,可以表示为:
klx=δxp-(l1+l2)・tan2εxq (2)
kly=δyp-(l1+l2)・tan2εyq (3)

由此可见:当传输距离(l1+l2)远远大于反射镜沿z 轴的扰动δn时,kl垌kzn, 沿z 的扰动相比旋转扰动可以忽略不计。至此,在忽略了反射镜绕z 轴扰动的基础上, 得到了光束失调量与反射镜位姿之间的计算关系如公式(4)、(5)所示:
εxq= 12 arctan((δxp-klx)/(l1+l2)) (4)
εyq= 12 arctan((δyp-kly)/(l1+l2)) (5)
当失调角度足够小时:
ε=12((δ-k)/l) (6)
2 减振技术原理性实验验证
通过减振技术原理性实验验证光路失调量与光路中快速响应反射镜位姿之间的计算模型。实验采用He-Ne 激光管作为光源, 分别经过装有作动器的反射镜和分光镜反射的光束传输至CCD,通过数据采集系统对失调光路进行实时检测, 实验装置如图5 所示。

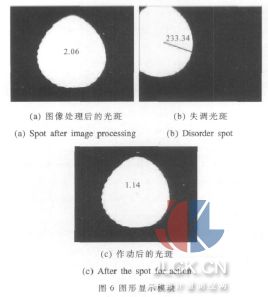
反射镜上装有两个new focus 8807 步进电机,电机1 控制俯仰, 电机2 控制扭转, 采用CCD(MINTRON)采集出射光斑。在振动干扰下,CCD 检测系统记录下光束在水平和垂直方向上的失调量;由光路失调计算模块对光斑失调量进行计算, 得到反射镜补偿量, 即电机1 作动反射镜的俯仰量及电机2 作动反射镜的扭转量; 通过电机完成对快速响应反射镜的控制, 同时,CCD 实时显示光斑的失调情况。CCD 检测振动失调光路调节过程如图6 所示。其中,图6(a)为经过图像处理定位后的光斑;图6 (b)为振动失调下的光斑位置;图6(c)为光路调节系统修正后的光斑位置。
依据CCD 检测到的光斑中心在x、y 方向上的失调量(总的传输距离50 cm),作动器作动反射镜补偿失调量的理论值和实际操作值对比如表1 所示。CCD、步进电机自身噪声和热噪声等都是造成误差的因素, 因此从表1 可以看出,由于步进电机是利用电磁铁原理,将脉冲信号转换成线位移或角位移的电机,每来一个电脉冲,电机转动一个角度,带动机械移动一小段距离。此实验通过计算所得到的反射镜位姿获取步进电机脉冲数,由于脉冲数为一整数,无论反射镜位姿如何变化, 所设计的步进电机作动量都是整数倍单位位移, 且大于或等于实际位移量。如公式(7)所示,N 表示步进电机脉冲数,X 表示反射镜位姿变化量,Y 表示步进电机单位位移量。

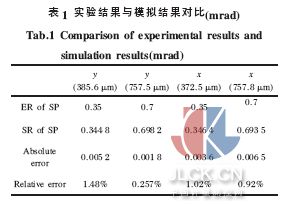
因此, 实验与和仿真结果的偏差均为正值且在系统允许范围内,实验验证了该减振技术的可行性。所采用的步进电机反应时间在百毫秒量级, 相比振动引起的光路失调时间要长得多, 通过步进电机对振动的实时控制还存在问题。相对而言,伺服电机的响应时间可达到毫秒量级,对于振动信号频率不高,在千赫兹以内的就可以采用文中的减振技术方案完成实时减振控制。鉴于所研究对象的主要干扰来自于低频信号( 百赫兹以内),减振调节时间比振动干扰周期快一个数量级,因此,该快速响应反射镜的主动减振技术可行,且计算方便,程序简单,电机控制可避免反复调节,提高时效。
3 结论
文中结合工程应用,提出了一种基于快速响应反射镜的主动减振技术。在对振动干扰下失调量分析计算的基础上, 推导出快速响应反射镜的系统作动量,控制并补偿其在振动干扰下的失调量,从而对振动失调光学系统实施减振。通过实验验证了减振方法的可行性,但要在实际应用中充分发挥作用,还需要高精度、高灵敏度、易集成的伺服电机及控制器和低噪声和高灵敏度的CCD 图像采集系统来提高主动减振系统的工作效率,达到实时反馈、实时减振的目的。
摘自:中国计量测控网







