测量数据统计学原理及表达(九)
发布时间:2017-09-01
在计算A类不确定度时应注意单次测量不确定度与测量列算术平均值不确定度的区别。
作为测量列中单次测量的不确定度可表示为U(x)=ta(n-1)s,这里ta(n-1)为与显著性水平α以及测量次数凡有关的因子,称为t分布的临界值或t分布的分位数,其值列于表2-18中。当测量为正态分布,且测量次数足够多时,对置信概率为99%(即显著性水平为1%),可取t=2.58,即单次测量的不确定度为2.58s。对置信概率为95%(即显著性水平为5%),可取t=1.96,即单次测量的不确定度为1.96s。
作为测量列算术平均值的不确定度可表示为![]() 其中n为测量次数。
其中n为测量次数。
(2)不确定度来源
化学分析测量不确定度的来源有以下几种:
①被测对象的定义不完善,例如被测定的物质缺少确切的结构说明。
②取样带来的不确定度,测定样品可能不完全代表所定义的被测对象。
③被测对象的预富集和分离的不完全。
④基体影响和干扰。
⑤在抽样、样品制备、样品分析过程中的沾污,这对痕量分析工作尤为重要。
⑥在对环境条件的影响缺乏认识或环境条件的测量不够完善,例如容量玻璃器具校准与使用时温度不同所带来的不确定度。
⑦读数不准,读取计数或刻度形成的习惯性偏高或偏低倾向
⑧称量和容量仪器等的不确定度。
⑨仪器的分辨率、灵敏度、稳定性、噪声水平、仪器的偏倚、检定校准中的不确定度以及自动分析仪器的滞后影响等。
⑩测量标准和标准物质所给定的不确定度值,特别是作为基准或标准用的试剂纯度的影响。有机纯物质由于同分异构体和无机盐的存在,在配制标准溶液时应考虑纯度这一重要因素。
(11)从外部取得并用于数据的整理换算的常数或其他参数的值所具有的不确定度。
(12)包括在测量方法和过程中某些近似和假设,某些不恰当的校准模式选择。例如使用一条直线校准一条弯曲的响应曲线,数据计算中舍、人影响。
(13)测量过程中的随机影响对不确定度的贡献。
所有这些影响不确定度的因素对总不确定度的贡献要做全面的分析评定,但有时这些因素之间并不一定都是独立的,所以必须考虑相互之间的影响对不确定度的贡献,即要考虑协方差。
(三)不确定度估计方式
①测量的数学模型建立对测量过程的全面了解。要了解测量是如何进行的,弄清被测量及其参数之间的关系,要对已知的系统性影响进行修正。由于大多数化学测量结果是在程序最终才获得的.因此要对中间量进行仔细研究,还需注意使用的常数。如果被测对象和其他量有函数关系
y= f(x1,x2,…,xn)
则这个关系的建立对评价被测对象的不确定度是重要的。要通过对x1,x2,…,xn等每一个量的不确定度给出y的不确定度。如果函数关系没有建立起来,就需要从实验或其他方式估计这些量对被测对象的影响,最终合成给出被汉0对象的不确定度。
②鉴别不确定度来源(见前述)并量化不确定度分量要对每一个不确定度来源通过测量或估计进行量化。实际上最大分量的1/3的那些分量是不用估计的,因此量化的第一步是要预先估计每一个分量对合成不确定度的贡献,排除那些不太重要的分量,这样就简化了不确定度分量的列表。
在很多情况下,不确定度分量随分析物的含量水平而变化。因此,确定不确定度程序应有所限制,即应在分析物含量水平附近的一个小范围内进行不确定度评估,或者给出含量水平与不确定度的相关性,然后计算出分析物含量水平下的不确定度。
对不确定度分量的量化可采用下述四种方式:
a.通过实验进行定量。
b.使用标准物质进行定量,此时需要考虑标准物质作为计量标准,其量值本身也有不确定度;在标准物质上所进行的测量的再现性;对标准物质测量所得测量值与该标准物质所具有的标准值之间的差异;标准物质成分和被分析样品成分之间的差异;测量系统对标准物质和被分析样品适应性的差异;取样所具有的不确定度。
c.基于以前的结果或数据的估计进行定量,包括来自供应商的信息、实验室之间的研究,熟练实验的结果、质量保证数据。
d.基于判断进行定量。

当误差限是由证书或其他说明书中得到,且没有明确给出确定的置信水平;当估计的误差限是以最大范围形式给出的,且没有对该误差的分布状况方面的知识时;当误差的性质偏重于系统性的误差时,建议按均匀分布处理。
当误差的性质偏重于随机性的,虽没有指定分布形式,但给出标准偏差或相对标准偏差(RSD)时;明确给出确定的置信水平的不确定度或置信区间,但没有指明分布,此时建议作为正态分布处理。 ③合成标准不确定度的计算
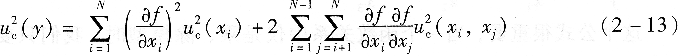
式中:uc(y)――y的标准不确定度;
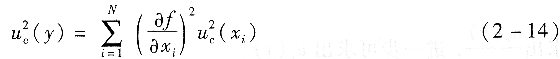
参考资料:标准物质定值原则和统计学原理







