测量数据统计学原理及表达(三)
发布时间:2017-09-01
3、表示一组数据离散程度的特征数
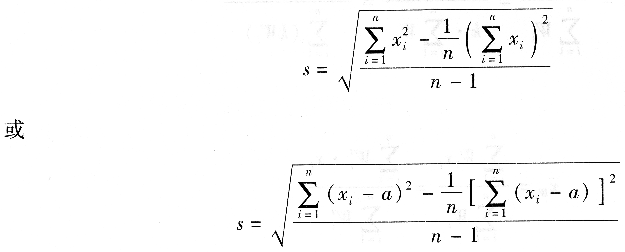
(1)标准偏差s
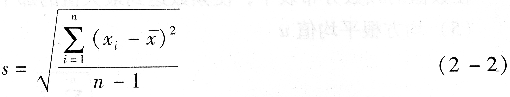

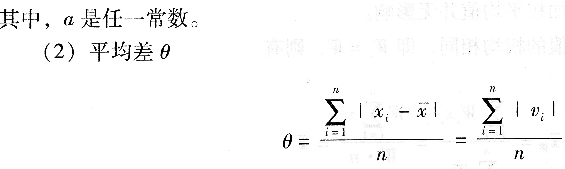
其中,vi=xi一x-称为第i个测量值的残差。
(3)极差R
极差是指一组观测值中最大值和最小值之差。
(4)或然误差ρ
或然误差是指在一组测量值的误差中,落在-ρ到+ρ范围内的误差个数与落在该区间之外的误差个数相等,或者说在所有的测量误差中,有一种误差,比它大的与比它小的误差的出现可能性恰好相等,这一误差就叫或然误差。
在数理统计中,用方差σ2来评价测量值与真值的偏离程度,若以μ表示被测量的真值,则有:
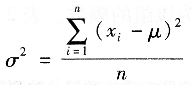
可以证明s2是σ2的无偏估计。由于标准偏差不仅是一组测量中各个观测值的函数,而且对一组测量中的较大误差感觉比较灵敏,故标准偏差为表示精度的较好方法。
若两组测量的残差分别为:

即按平均差表示两组数据离散程度相同。
但若按标准偏差表示:
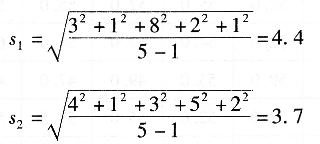
由此可见,第一组中比较突出的大误差在标准偏差中就可以较好地反映出来。
用极差表示的缺点是它仅取决于两极端值,而与测量次数无关,因此它所使用的一组数据的信息就少得多。
根据或然率理论,当测量次数相当大时,则有如下关系:
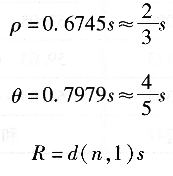
在正态分布时,d(n,1)值可由表2―5中查出。

在通常情况下,计算s时,采用式(2―2)为最好。该式亦称为贝塞尔(Bessel)公式。
4、正态分布及其检验
如将一个量的测量结果按由小到大的顺序排列,并按照一定的问隔将其分成若干组时,则每一组中测量数据的数目称为该组的频数。表2―6、表2―7列出某物质中铜含量分析结果及其分布。
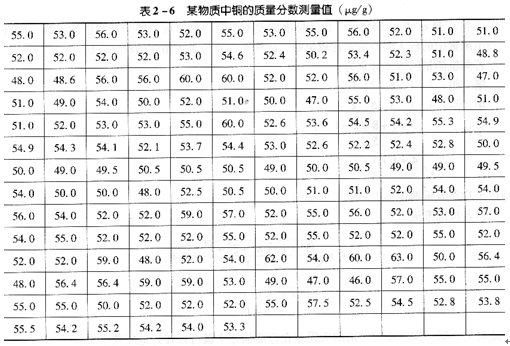
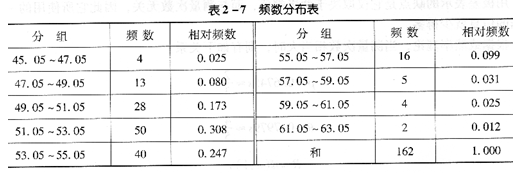
从表2―7中可以看出测量值的波动规律。为更直观起见,以横坐标表示测量值的大小,标出分组的点;以纵坐标表示频数,画出一个个矩形,这个图称为频数分布直方图(见图2―2)。频数与总的测定次数之比称为相对频数,同样可以作出相对频数分布直方图(见图2―3)。
参考资料:标准物质定值原则和统计学原理







