测量数据统计学原理及表达(二)
发布时间:2017-09-01
二、数理统计中的基本概念
1、测量误差及其分类
由测量所得到的被测量值与被测量的真值之间的差叫做测量误差。测量误差可以用这个差值来表示,也可以用该差值与被测量的真值之比来表示,所谓被测量的真值是指一个量在被观测时,该量本身所具有的真实大小。由于被测量的真值一般来说是不知道的,所以选择真值的最佳估计值以及确定该估计值的误差就是数据处理中的首要问题。
按照误差的性质及产生的原因,通常可将误差分为三类:偶然误差(或随机误差)、系统误差和疏失误差。
假定对一个量作n次测量,测得数据为:

偶然误差是指在实际测量条件下,多次测量同一量时,误差的绝对值和符号以不可预定方式变化着的误差。当测定次数足够多时,出现数值相等、符号相反的偏差的概率近乎相等,各种大小偏差出现的概率遵循着统计分布规律。例如,遵从正态分布的误差具有以下几个特点:
(1)单峰性:绝对值小的误差出现的概率比绝对值大的误差出现的概率大;
(2)对称性:绝对值相等的正误差和负误差,其出现的概率相等;
(3)有界性:绝对值很大的误差出现的概率近于零,亦即误差有一定的实际限度;
(4)抵偿性:在实际测量条件下对同一量的测量,其误差的算术平均值随着测量次数增加亦趋于零。
引起偶然误差的因素是无法控制的。虽然不能找到适当的因数对偶然误差予以校正,但可以通过增加测定次数在某种程度上将它减小。
系统误差是指在同一条件下多次测量同一量时,误差的绝对值和符号保持恒定,或在条件改变时,按某一确定的规律变化的误差。对于那些绝对值和符号保持恒定的已定系统误差,可以按照它作用的规律,对它进行校正或设法消除它。对那些不能确定的但其值又足够大的系统误差,在计算测量的总误差时予以估计并和其他误差进行合成。企图增加测量次数是不能使系统误差减小的。
疏失误差是指那些超出在规定条件下预期的误差,是一种显然与事实不符的误差,主要是由于工作人员的疏忽或测量仪器的不正确使用所造成的。这是在测量过程中应避免的一类误差。
反映系统误差的大小常用“正确度”一词;反映偶然误差的大小常用“精密度”一词。图2―1说明它们之间的区别。
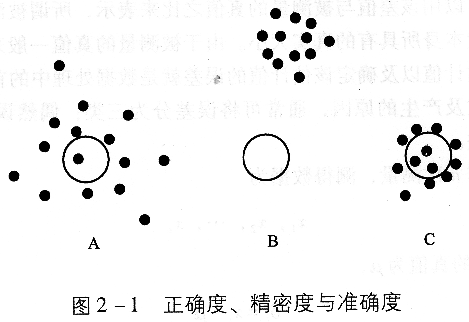
图2―1中A表示系统误差小,而偶然误差大,即正确度高而精密度低;B表示系统误差大,而偶然误差小,即正确度低而精密度高;C表示系统误差与偶然误差均小,即准确度高。
应该注意到,由于被测量的真值在绝大多数情况是未知的,因此误差应该理解为是一个定性的概念,而不应该理解为是一个定量的概念,所以严格说来误差只能说高低、大小,而不应表达为诸如0.1或l%等。
2、表示一组数据集中位置的特征数
假设一个分析工作者用某一分析方法对标准物质的某一特性做出一组等精度测量,测得数据为:xl,x2,…,xn。
(1)算术平均值x-:

(3)中位数M
将观测值按由小到大的顺序排列,属于中间位置的测量值称为中位数(若测量个数为偶数,则为居中的相邻两数的平均值)。
(4)众数M0
在数值的频数分布表中,使频数达到最大值的那个数值即为众数。
(5)均方根平均值u

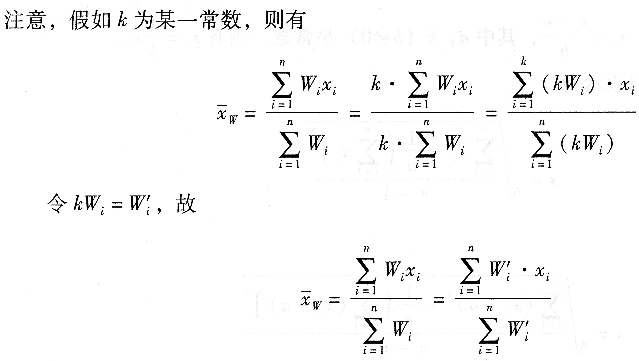
也就是说权同时乘一个常数对加权平均值并无影响。
另外,假若一个加权平均值的权均相同,即Wi=W,则有:
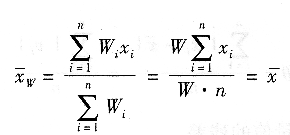
也就是说当权完全相同时,加权平均值和算术平均完全相同,即算术平均值是加权平均值权完全相同的一种特例。
(7)调和平均数H
![]()
按照数理统计理论,测量值在服从正态分布情况下,可以证明算术平均值x-为测量结果的最佳值。它是最常用的表示集中位置的特征数,因此通常都是用算术平均值来表示测定结果。
参考资料:标准物质定值原则和统计学原理







