定量分析中的误差(一)
发布时间:2017-09-01
分析结果与真实值之间的差值称为误差。分析结果大于真实值,误差为正;分析结果小于真实值,误差为负。
根据误差的性质与产生的原因,可将误差分为系统误差和偶然误差两类。
一、系统误差和偶然误差
1、系统误差
系统误差是由某种固定的原因所造成的,其数值具有单向性,即在同一原因的影响下,其测定结果总是系统地偏高或偏低;当重复测定时,会重复出现,且误差大小基本不变,对测定结果影响比较恒定。因此系统误差的大小、正负是可以测定的,至少在理论上说是可测的,因此系统误差又称为可测误差。产生系统误差的原因主要有以下几个方面。
(1)方法误差
指分析方法本身所造成的误差。例如,重量分析中由于沉淀的溶解损失,会使分析结果偏低;而由于杂质的包藏,又会使分析结果偏高。又如滴定分析中反应进行不完全,或由于指示剂选择不当造成的终点与化学计量点不一致等,也都会产生系统误差。
(2)仪器误差
指仪器本身的缺陷造成的误差。例如,分析天平两臂不等,砝码未经校正,滴定管刻度不准,容量瓶与移液管未经相对校正等,在使用过程中就会引入误差。另外,玻璃或塑料容器所含杂质的溶出,也往往造成误差。
(3)试剂误差
所用化学试剂或蒸馏水中若含有微量的待测组分或对测定有干扰的杂质,会造成测定误差,对微量、痕量分析造成的影响尤为严重。作为基准物的物质纯度达不到要求,也会造成系统误差。
(4)主观误差
由于操作人员主观原因造成的误差。例如,不同的分析人员判断颜色的能力不同,对终点颜色辨别偏深或偏浅;有的分析人员为了使测定结果的重复性好,在读数时常常带有主观倾向性,总是想使第二次体积读数与第一次的体积读数相吻合,不自觉地受到“先人为主”的影响,结果造成主观误差。
2、偶然误差
偶然误差产生的原因与系统误差不同,它是由某些难以控制、无法避复的偶然因素(如测定时仪器性能的微小变化,环境的温度、湿度和气压的微小波动等)造成的,其大小、正负都不固定,完全是随机的。因此这种误差也称为随机误差或不可测误差。虽然偶然误差难以觉察和控制,但是消除系统误差后,在同样条件下进行多次平行测定,则可发现偶然误差的分布也是服从一定规律的。
①大小相等的正、负误差出现的概率相等。
②小误差出现的概率大,大误差出现的概率少。
虽然偶然误差不能通过校正而减小或消除,但可以通过增加测量次数予以减小。不存在系统误差的情况下,测定次数越多其结果平均值越接近真值。实验表明,在测定次数较少时,偶然误差随着测定次数的增加而迅速减小,当测定次数大于10时,偶然误差已减小到很小的数值。所以,一般平行测定4~6次就可以了。
除这两种误差外,往往可能由于分析人员的粗心大意或违反操作规程等而造成“过失误差”。如器皿不洁净、溶液溅失、转移沉淀时丢失、加错试剂、看错砝码、读错滴定管读数、记录或计算错误等,这些都属于不应有的过失,是错误而不是误差,必须避免。在处理所得数据时,如发现确实为过失引起的错误,应该把该次测定的结果弃去不要,重新测定。因此,在定量分析测试的工作中,首先必须掌握规范的操作技术,其二就是必须要有严谨求实、一丝不苟的科学态度。
二、真值、平均值、中位数
1、真值(用µ表示)
某一物理量本身具有的客观存在的真实数值,即为该量的真值。一般来说,真值是未知的。但下列情况的真值可认为是已知的。
(1)理论真值
比如某纯物质的理论组成或含量,如纯NaCl中Cl的含量(质量分数):
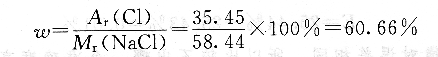
(2)约定真值
如国际计量大会上确定的长度、质量等;标准参考物质证书上给出的数值;有经验的人在确认消除系统误差后用可靠方法多次测定的平均值。
(3)相对真值
认定精确度高一个数量级的测定值可作为低一级测量值的真值(如在仪器分析中常常用标准试样的含量作真值)。
2、平均值(x
相同条件下,n次测定结果的算术平均值,即:
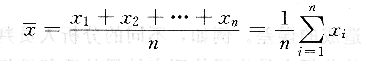
算术平均值虽然不是真值,但是比单次测定结果更接近真值。分析工作中常常用多次测定的算术平均值来代替真值。数理统计方法已经证明,在没有系统误差的前提下,一组测量数据的算术平均值就是真值的最佳估计值。
3、中位数(xM)
一组测量数据按大小顺序排列,中间一个数据即为中位数xM。当测量值的个数为偶数时,中位数为中间相邻两个测量值的平均值。
参考资料:分析化学







