标准曲线的回归分析
发布时间:2017-09-01
一、一元线性回归方程
在分析化学中,经常使用标准曲线来获得试样某组分的浓度。如光度分析中的浓度-吸光度曲线;电位法中的浓度一电位值曲线等。怎样才能使这些标准曲线描述得最为准确,误差最小呢?这就需要找出浓度与某特征值两者之间的定量关系以及代表这种关系的回归方程。以下简介回归方程的计算方法。
设浓度x为自变量,某特征参数了为因变量,在x与y之间存在一定的相关关系,当用实验数据xi和yi绘图时,由于测量仪器本身的精度以及测量条件的微小变化等都会给测量带来误差,因此用各测量点的测量值绘图就不可能全部在一条直线上,而是分散在直线的周围。为了找出一条直线,使各实验点到直线的距离最短,即误差最小。需要用数理统计方法,利用最小二乘法计算出相应的方程yi=a+bxi后再绘出相应的直线,这样的方程称为y对x的线性回归方程,相应的直线称为回归直线,从回归方程或回归直线上求得的数值,误差小,准确度高。式中的a为直线的截距,与系统误差大小有关;b为直线的斜率,与方法灵敏度有关。
设实验点为(xi,yi)(i=1→n),则平均值:

由最小二乘法得:
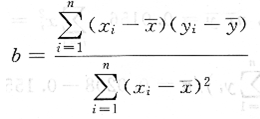
或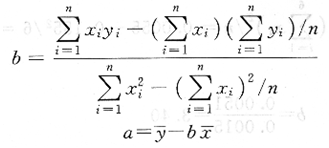
若a、b值确定,回归方程也就确定了。但这个方程是否有意义,还需要判断两个变量x与y之间的相关关系是否达到一定密切程度,因为即使数据误差很大,仍可以求出一回归方程。为此可采用相关系数(r)来检验。
二、相关系数
相关系数r由下列公式计算:
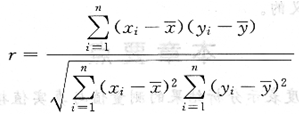
当r=1时,两变量完全线性相关,实验点全部在回归直线上。
R=0时,两变量毫无相关关系。
0<|r|<1时,两变量有一定的相关性,只有当|r|大于某临界值时,二者相关才显著,所得的回归方程才有意义。
r的临界值与置信度及自由度有关,如表所示。如果计算的r大于表上相应数值,则表示所求的回归直线方程有意义;反之,则无意义。
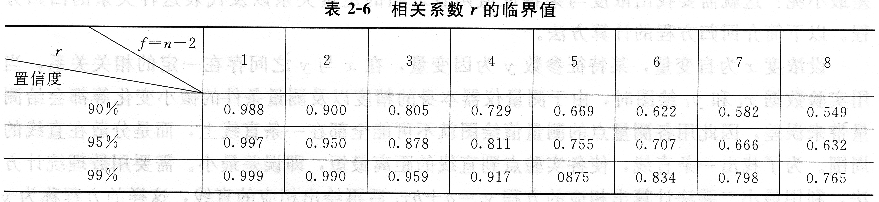
参考资料:分析化学







